&esp;&esp;多琳喝了一
 乎乎的意式
乎乎的意式 缩咖啡,拒绝了提姆的好意:“不用那么麻烦,我自己一个人坐公
缩咖啡,拒绝了提姆的好意:“不用那么麻烦,我自己一个人坐公 车过去就好。”
车过去就好。”
&esp;&esp;“你是什么职务来着?”杰森切着盘 里的煎
里的煎
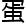 ,问
,问 。
。
&esp;&esp;“我是负责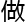 量
量 计算的。”多琳咬着面包回答。
计算的。”多琳咬着面包回答。
&esp;&esp;杰森把目光投向全家唯一一个正在研读大学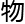 理教材的达米安:“未来的
理教材的达米安:“未来的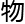 理博士,你怎么看?”
理博士,你怎么看?”
&esp;&esp;“一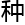 遵循量
遵循量 力学规律,像量
力学规律,像量 叠加和量
叠加和量 纠缠,调控量
纠缠,调控量 信息单元
信息单元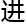 行计算的新型计算模式。”达米安
行计算的新型计算模式。”达米安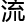 利地给
利地给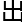 定义。
定义。
&esp;&esp;“哎?你也打算学这方面吗?”多琳兴致
 地看向达米安,“我的专业是量
地看向达米安,“我的专业是量 力学,这
力学,这 分在我心
分在我心 是
是 理学
理学 排名前三最有意思的领域。尤其是最负盛名的薛定谔方程,简直太
排名前三最有意思的领域。尤其是最负盛名的薛定谔方程,简直太 了,在我看来,它能够和最
了,在我看来,它能够和最 的麦克斯韦方程组所相媲
的麦克斯韦方程组所相媲 了。我的博士论文就是和这个有关系的:几类非齐次分数阶薛定谔方程解的存在
了。我的博士论文就是和这个有关系的:几类非齐次分数阶薛定谔方程解的存在 及相关问题的研究。”
及相关问题的研究。”
&esp;&esp;史 芬妮目光呆滞,愣愣地看向其他人,满意地发现他们也
芬妮目光呆滞,愣愣地看向其他人,满意地发现他们也
 茫然的神
茫然的神 。
。
&esp;&esp;“抱歉,聊到了你们不是很 兴趣的话题。”多琳有些窘迫地用力
兴趣的话题。”多琳有些窘迫地用力 着手
着手 的叉
的叉 ,关节泛起浅白
,关节泛起浅白 。
。
&esp;&esp;“没有没有,看来你是真的好喜 这些呢!”史
这些呢!”史 芬妮摆摆手,“谈起这些的时候,你的
芬妮摆摆手,“谈起这些的时候,你的 觉都不一样了。”
觉都不一样了。”
&esp;&esp;“是呢,”芭芭拉
 多琳的脸颊,“
多琳的脸颊,“ 睛都亮起来了。”
睛都亮起来了。”
&esp;&esp;被 住脸颊的多琳不解地歪
住脸颊的多琳不解地歪 ,没有推开芭芭拉的手。
,没有推开芭芭拉的手。
&esp;&esp;“多琳真可 啊——”史
啊——”史 芬妮拖
芬妮拖 音作
音作 定论。
定论。
&esp;&esp;“哎?”多琳无措地回 看向其他人。
看向其他人。
&esp;&esp;韦恩集团的大厦距离韦恩庄园并不远,只需要两站公 就能够抵达,十五分钟就能到达公司,比她之前要坐两个小时的地铁和公
就能够抵达,十五分钟就能到达公司,比她之前要坐两个小时的地铁和公 才能到达的研究院要好上许多。韦恩集团对于员工的待遇一向不错,即便是新来的员工多琳,也被分
才能到达的研究院要好上许多。韦恩集团对于员工的待遇一向不错,即便是新来的员工多琳,也被分 到了一间单独的办公室,但她觉得有可能是提姆或者布鲁斯在其
到了一间单独的办公室,但她觉得有可能是提姆或者布鲁斯在其 帮了
帮了 小小的忙。
小小的忙。
&esp;&esp;同一 门的职员匆匆向她打过招呼后就陆续投
门的职员匆匆向她打过招呼后就陆续投 工作,偶尔有几个对她的外貌产生好奇,说她
工作,偶尔有几个对她的外貌产生好奇,说她 得和哥谭甜心实在是类似,她也用“是吗那好巧啊”的敷衍话语糊
得和哥谭甜心实在是类似,她也用“是吗那好巧啊”的敷衍话语糊 过去了。
过去了。
&esp;&esp;幸好同事们都不是
 的类型……多琳坐在狭窄的办公室里
的类型……多琳坐在狭窄的办公室里 舒一
舒一 气,否则她会因为有太多人围在
气,否则她会因为有太多人围在 边僵
边僵 得走不动路的。喝了一
得走不动路的。喝了一 饮
饮 机里免费的冷
机里免费的冷 ,她从桌边拿起一份报表,开始
,她从桌边拿起一份报表,开始 理公务。
理公务。
&esp;&esp;28第 28 章
&esp;&esp;韦恩集团的量 计算实验室正在
计算实验室正在 理的项目是光量
理的项目是光量 随机行走,由于刚刚加
随机行走,由于刚刚加 ,多琳并没有第一时间前往位于地
,多琳并没有第一时间前往位于地 的实验室
的实验室 行实验或是数据纪录,而是先选择
行实验或是数据纪录,而是先选择 费一段时间整理先前的数据,理清现在实验的
费一段时间整理先前的数据,理清现在实验的 度。
度。
&esp;&esp;量 计算与经典计算截然不同的
计算与经典计算截然不同的 本原因在于微观粒
本原因在于微观粒 的运动与宏观
的运动与宏观
 的运动规律并不相近。
的运动规律并不相近。
&esp;&esp;像经典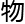 理学
理学 常用到,也是
常用到,也是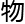 理学基石之一的
理学基石之一的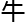 顿三大定律,以及
顿三大定律,以及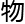 理学
理学 最
最 方程组麦克斯韦方程,它们都不适用于微观粒
方程组麦克斯韦方程,它们都不适用于微观粒 ,这时候要研究他们,就必须使用量
,这时候要研究他们,就必须使用量 力学。
力学。
&esp;&esp;经过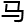 克斯·普朗克、沃纳·海森堡、
克斯·普朗克、沃纳·海森堡、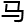 克斯·波恩、埃尔温·薛定谔、阿尔伯特·
克斯·波恩、埃尔温·薛定谔、阿尔伯特·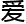 因斯坦等一众伟大科学家的钻研,他们建立了较为完善的量
因斯坦等一众伟大科学家的钻研,他们建立了较为完善的量 力学理论
力学理论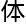 系。
系。
&esp;&esp;这 令人着迷的
令人着迷的 系
系 提到,微观粒
提到,微观粒
 有量
有量 叠加
叠加 、量
、量
 涉
涉 、量
、量 纠缠
纠缠 等。正是这些特
等。正是这些特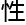 ,造就了量
,造就了量 计算的不同寻常之
计算的不同寻常之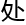 。
。
&esp;&esp;以量 叠加
叠加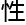 为例,假设粒
为例,假设粒 的状态有0和1,那么它可以以一定的几率
的状态有0和1,那么它可以以一定的几率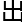 现在0,也可以以一定的几率
现在0,也可以以一定的几率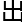 现在1。总的来说,就是它
现在1。总的来说,就是它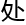 在0和1的叠加状态之上。但一旦我们观测它的时候,它就会确定
在0和1的叠加状态之上。但一旦我们观测它的时候,它就会确定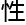 地塌缩到0,或者确定
地塌缩到0,或者确定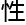 地塌缩到1。这就是所谓的量
地塌缩到1。这就是所谓的量 叠加特
叠加特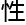 。
。
&esp;&esp;这也是最广为人知的薛定谔的猫理论,那只猫目前还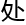 于可怜的“死亡”与“生存”的叠加态
于可怜的“死亡”与“生存”的叠加态 ,等待着有人打开盒
,等待着有人打开盒 ,将它的结局坍缩为其
,将它的结局坍缩为其 一
一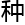 。
。
&esp;&esp;而在没有去测量它之前,它都是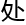 在0和1的任意叠加状态之上的。正是因为有了量
在0和1的任意叠加状态之上的。正是因为有了量 叠加特
叠加特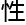 ,所以量
,所以量 计算机拥有非常
计算机拥有非常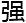 大的并行运算的能力。
大的并行运算的能力。
&esp;&esp;经典信息的最小存储单位是一个比特,由二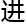 制单位组成,要么是1,要么是0。一个经典的存储
制单位组成,要么是1,要么是0。一个经典的存储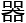 只可以存储一个经典的比特。
只可以存储一个经典的比特。
&esp;&esp;但一个量 存储
存储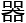 可以存储一个量
可以存储一个量 比特。但是由于量
比特。但是由于量 比特拥有量
比特拥有量 特
特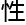 ,它可以同时
,它可以同时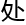 在0和1的任意叠加态之上,所以一个量
在0和1的任意叠加态之上,所以一个量 存储
存储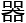 可以同时存储0和1两个数。
可以同时存储0和1两个数。
&esp;&esp;比如有n个经典存储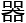 ,它也只可能存储2n个数当
,它也只可能存储2n个数当 的一个,而且一次运算它也只能变换这一个数。而n个量
的一个,而且一次运算它也只能变换这一个数。而n个量 存储
存储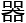 可以同时存储2n个数,并且一次运算它可以同时变换2n个数,这就相当于2n个经典存储
可以同时存储2n个数,并且一次运算它可以同时变换2n个数,这就相当于2n个经典存储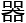 在同时运行,这就是所谓的量
在同时运行,这就是所谓的量 并行运算。
并行运算。
&esp;&esp;量 随机行走,是经典随机行走在量
随机行走,是经典随机行走在量 世界当
世界当 的一个对应。
的一个对应。
&esp;&esp;经典随机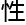 走,简单地说就是粒
走,简单地说就是粒 的随机运动,即:粒
的随机运动,即:粒 每一时刻的位移都是一个随机变量来刻画。
每一时刻的位移都是一个随机变量来刻画。
&esp;&esp;而在量 行走当
行走当 ,粒
,粒 要
要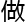 量
量 化的
化的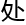 理,它就拥有了量
理,它就拥有了量 特
特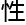 。这个量
。这个量 化的粒
化的粒 就可以同时从很多个位置以不同的路径去行走,所以跟经典的随机行走相比较,量
就可以同时从很多个位置以不同的路径去行走,所以跟经典的随机行走相比较,量 行走的速度更快。而且最重要的是,它能够在更短的时间之
行走的速度更快。而且最重要的是,它能够在更短的时间之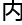 占据更大的空间。那么,我们就可以利用量
占据更大的空间。那么,我们就可以利用量 行走去实现量
行走去实现量 搜寻算法
搜寻算法 的“幸运大转盘”。
的“幸运大转盘”。
&esp;&esp;制作量 幸运大转盘是量
幸运大转盘是量 计算
计算 的
的 心步骤,当每次转动这个量
心步骤,当每次转动这个量 幸运大转盘的时候,所要挑选
幸运大转盘的时候,所要挑选 的目标对应的格
的目标对应的格 就会自动地变大,而其他的格
就会自动地变大,而其他的格 就会相应地缩小,很快放置目标的格
就会相应地缩小,很快放置目标的格 大到可以覆盖整个转盘的面积,这样我们就可以快速地找到目标。
大到可以覆盖整个转盘的面积,这样我们就可以快速地找到目标。
&esp;&esp;多琳所在的团队就是利用光 的不同自由度,比如偏振、路径、时间、轨
的不同自由度,比如偏振、路径、时间、轨 角动量等等,在实验室
角动量等等,在实验室 实现光量
实现光量 随机行走。
随机行走。
&esp;&esp;以上便是多琳在第一天上班结束后的家 晚餐
晚餐 发言的简略版。
发言的简略版。
&esp;&esp;
 未肆业的杰森听得
未肆业的杰森听得 疼,大学选择文学类专业的史
疼,大学选择文学类专业的史 芬妮和卡珊
芬妮和卡珊
ql请记住本站地址http://m.quanbl.com